Unit 5 Summary 

Work:

We started this unit of by talking about a thing called work. Well what is work you ask?  Good
question, thank you for asking.  Work is a transfer of energy and is responsible for generating power.   Work is the result of Force multiplied by distance.
                                                                                                 work = F x d 
The resulting work is measured in what are called Joules.  An example of this would be:
               If a man weighs 900 Newtons, and he goes up stairs that are 7 meters high, how much work was done?
            This is easy, we just plug in our force (900N)  x  Our distance (7m) =  6300J of work.
There is on final catch however.  the forces in work must be parallel or they will NOT generate work.

Power:  

Now that we understand work we can talk about power.  Power is determined by how quickly work is done.             The formula for this is
                                                             Power = work/time 
And power is measured in what are called watts.    no Not all pro defensive end for the Texans             JJ Watt    
Although he does generate a lot of power.

As an example, lets use our first question with work, and find how much power was generated.

 SO we know that we had done 6300J of work, and lets say that it had taken the man 10 seconds to climb the stairs.
Lets set up the equation:
   Power = 6300/10  =  630 watts

Congratulations you now can move from work all the way to power!  but we are not done yet.


Kinetic Energy: 

Energy is an objects ability to do work.  And kinetic energy is an energy that requires movement and is found by the equation below.
                                                    KE= 0.5(m)(v)^2 
So here is the funny thing about physics, its all connected.  So that work that we learned about earlier, yeah its coming back again.  Thats because another way to find work is by the change in kinetic energy.
what this looks like is                          Work = DeltaKE   (delta = change in)
And how is it that we find the change in KE?  By the formula below, that's how.
                                                                 Delta KE = KE final - KE initial 

So lets do an example shall we?

A 10 kg mouse is running at 5 meter per second.  How much kinetic energy does the mouse have?

Well first lets set up our equation.   KE= 0.5(m)(v)^2  and now lets fill it in with the information that we have.                                           KE= 0.5 (10)(5)^2
That leave us with                            KE= 125J                  And KE is measured in Joules as well.



Potential Energy:

Potential energy is a tricky one. This is because it is not actually energy.  Instead, potential energy is exactly what it sounds like, the potential that an object has to have energy.
That's kinda confusing, I understand.  So lets break it down shall we?

Potential Energy = mass x gravity x height.   So the potential energy of an object depends on three (but really just two) things.   The objects mass and the objects height.  Gravity is also important but because earths gravity is the same on everything it is not a variable to potential energy.  

Further more, the mass of an object does not simply change, and so the thing that determines an objects PE is its height.  As soon as the object leaves the ground it has a potential energy that increases as it gets higher from the ground.

And although height is an important factor in PE.  It is important to understand that movement is not required for potential energy.



Machines: 

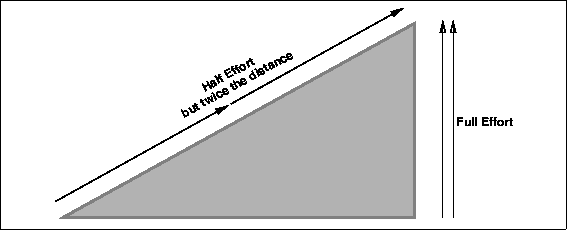
Machines are fairly simple, especially the simple machines. "ba dum tisssssss"  bad jokes aside, there really is not to much to a machine.  At the end of the day, the machines job is to make the work you do easier.   But here is the catch, a machine does not make work less,  it only makes the force required in the work less.

We know that work = force x distance.  And so to decrease the force we must increase the distance.  We know that work in must equal work out, so we can not do any less work, but we can change how we do the work.  
For example a ramp.   A ramp increases the distance that an object covers meaning that it took less force to accomplish the same amount of work.

Mass of Meter Stick Challenge 

The challenge was to find the mass of a meter stick only using a table, a 100g weight, and the meter stick itself. 

The first step was to get the meter stick to balance on the edge of the table while the 100g weight was on one end  This looked something like the image below. 

To balance the stick we had to create a clock-wise torque that was equal to the counter clock-wise torque. Because torque = force x lever arm    we had to find the force of the end of the stick with the weight.   

Because we know that weight = mass x gravity we plugged that in to get the equation

                                                         weight = 100 x 9.8  =  980

 And at this time the length of the lever arm was 30 cm on the left side, and was 20 cm on the right because it extended to the center of gravity on the meter stick.  
Now that we have this we can plug in our equation:
                                                          980 x 30 = X  x  20
After solving this equation we discover that the meter stick has a mass of 1470 and we then convert this into grams by simply moving the decimal point to the left. this leaves us with 147 grams.

Unit Summary #4

We started this unit with the concept of Rotational Inertia.  Before we explain what Rotational Inertia is lets have a refresher of what inertia alone is.  

                            Inertia = the property of an object to resist changes in motion 

Now that we have been reminded of what inertia is, lets look at Rotational inertia.

                        Rotational Inertia = the property of an object to resist changes in spin

One factor that has a great impact on rotational inertia is the location of mass.   For example: 

                                

When the mass is placed closer to the axis of rotation it is easier to rotate

Conservation Of Angular Momentum

Conservation of angular momentum (otherwise known and rotational momentum) states that the angular momentum before is equal to the angular momentum after.    But what is angular momentum?

                           Angular momentum = rotational inertia x rotational velocity


Here is a video that my group made explaining this concept.
  

         

Tangential and Rotational Velocity

Have you ever wondered how trains stay on the tracks when they take a curve?  No, you haven't?  Well to bad, you're going to learn about it anyways. There are two major factors that keep the train on the tracks: Rotational Velocity, and Tangential Velocity. 

Rotational Velocity = how fast something rotates around its axis of rotation.

Tangential Velocity = How fast something would be moving it were traveling in a straight path. 

     

Take a look at this photo.  Do you see how the wheels are connected by the axle and do not rotate independently.  Also notice how the wheels are shaped.  How they taper, being wider on the inside and smaller on the outside.

Because the wheels are connected by an axle, they have the same rotational velocity. however, different parts of the wheels have different tangential velocities.

The parts of the wheel that are wider have so spin faster (thus having a greater rotational velocity) in order to keep of with the skinny parts of the wheels who do not have to go as fast to have the same rotational velocity.  

 So when the train comes into a curve, one side has its wheels touching the tracks with only its slower spinning narrow portion. And the other has its wider and faster spinning parts of the wheels touching the track.   What this causes is the wheels that are on the side of the train  spin faster, and push the train back into the center of the tracks.

Torque

Torque is a force that causes an object to rotate.    In case you did not know, when you fall over you are actually rotating and this is all about torque.   But what is torque?

                                                                                                  Torque = Force x Lever Arm 

What this equation tells us is that you can achieve a large torque either by a large force, or by a large lever arm. 

When you are trying to rotate a difficult bolt with a wrench.  You are already applying as much force as you can so what can you do to generate more torque?  If you said lengthen the lever arm then you are correct.  Because we know that torque = force x lever arm we can increase the torque on the bolt by adding a pipe to the end of the wrench, or by getting a longer wrench.

Another thing torque is responsible for is balance.
Balance is achieved  when the counter-clockwise torque = the clockwise torque.
                                     
Because torque can be hanged by either force or lever arm, the forces nor lever arms have to be equal in order to balance. All that is required is that their product on each side of the axis of rotation are equal to each other.

Center of Mass

Center of mass = average position of all an objects mass.  Also called the center of gravity, the center of mass is very important when it comes to things falling over or not falling over. For something to fall over, it must have its center of mass outside of its base of support. 

When a person is standing as this man in the picture is, they do not have a very wide base of support meaning that they would not have to rotate very far in order to place their center of gravity outside of their base of support.  

A famous example of this is the leaning tower of Pisa.
.          
As we can see. The tower is leaning a great amount, however it is not falling over because it still has its center of mass inside of its base of support.